Gabriel Cramer's Rule
Applying Kirchhoff's Voltage Law to each loop in a guitar amp circuit results in one equation per loop. These equations need to be solved simultaneously to determine the answer that we seek, which is typically the output voltage as a function of the input voltage. Let's look at an example and solve it using a crude, but workable method known as simple substitution. Later we will demonstrate how a concept called Cramer's Rule can make life easier and less prone to math errors.
Problem
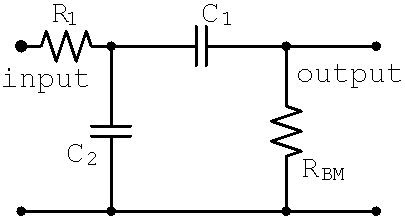
Consider the tonestack of the Sovtek MIG 50 Master Volume, which is the same as the Fender Bassman 5F6-A except for part values. At bass frequencies the treble bleed capacitor acts as an open circuit. If we set the treble and midrange controls to minimum and the bass control to maximum then the effective circuit is shown below. What is the relationship between the output voltage and the input voltage under these conditions?

|
Guitar Amplifier Electronics: Fender Deluxe - from TV front to narrow panel to brownface to blackface Reverb |
Solution
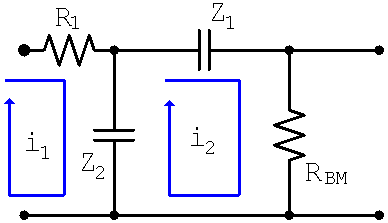
For the MIG 50 the parts values are R1 = 51k, C1 = 0.022uF, and C2 = 0.047uF. With the 1M bass control at maximum and the 25k midrange control at minimum they are in series and thus form an equivalent resistance of RBM = 1.025M. We form two loops, one for the current i1 and the other for i2
The impedances of the capacitors are purely imaginary. (True, but what a strange statement when taken out of context!) For a frequency of 100Hz, for example, they are
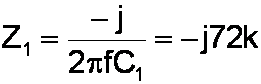
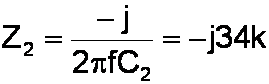
In the first loop there is one voltage rise: the input voltage. There are two voltage drops due to R1 and Z2, which from Ohm's Law are the impedances times the current. Notice that Z2 has a voltage drop caused by the current i1 in the first loop, but a voltage rise caused be the current i2 in the second loop that is flowing in the opposite direction through the capacitor. The current i2 must therefore be subtracted from i1 in determining the voltage drop. According to Kirchhoff's Voltage Law, the sum of the voltages rises is equal to the sum of the voltage drops:
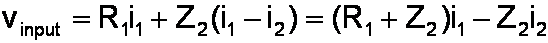
Notice in the second step that we have combined the currents together. This is usually the most convenient form.
In the second loop there are no voltage rises and the voltage drop across Z2 is caused by the current i2 minus the current i1:
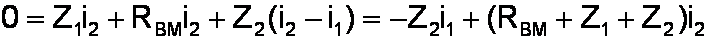
We are interested in the output voltage, which from Ohm's Law is RBM times i2. So we use the equation for the second loop to get
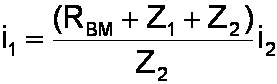
and then substitute this result into the equation for the first loop, thereby eliminating the unknown current i1 that we don't need to know. Now we have the input voltage as a function of only the current i2.
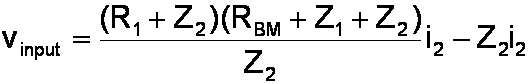
which simplifies to
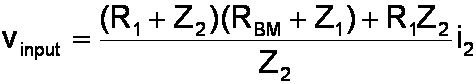
We re-arrange the equation to compute the current as a function of the input voltage:
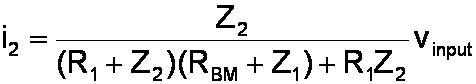
By Ohm's Law the output voltage is RBMi2.
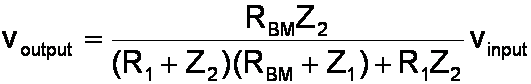
We achieved our result. We now have the output voltage as a function of the input voltage and the impedances. The clunky procedure we used, eliminating one of the unknown currents by substitution, was as appealing as cold solder on a turret board.

|
Guitar Amplifier Electronics: Basic Theory - master the basics of preamp, power amp, and power supply design. |
Aside from being of low esthetic value, a procedure like this leaves you prone to making mistakes. What we need is a more elegant approach that is less likely to produce errors. Full blown matrix mathematics is the ultimate method in this regard, but for tube amplifiers a method known as Cramer's Rule is quite sufficient.
Cramer's Rule
Gabriel Cramer's Rule handles 90 percent of the equations we saw in our Sovtek MIG 50 problem. We use Kirchhoff's Voltage Law for both loops, just as before. Then Cramer's Rule gives us the current i2 in the second loop as a function of the input voltage. At that point all we do is apply Ohm's Law to get the result.

Here is how it works.
We still need to apply Kirchhoff's Voltage Law to the two loops. Each of the two resulting equations has one or more voltage rises caused be voltage sources and voltage drops caused be impedances and currents.
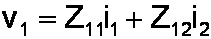
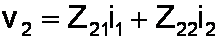
Either of the voltages could be zero. Each of the impedances Z11, Z12, Z21, and Z22 can be a single value, a sum of impedances, or zero.

|
Fundamentals of Guitar Amplifier System Design - design your amp using a structured, professional methodology. |
We stack these two equations into a matrix like this

To mathematicians this matrix says exactly the same thing. It simply expresses our two separate equation as one big equation with only one equal sign. There are two diagonals in the impedance matrix, one going from the upper left at Z11 to the lower right at Z22. The second diagonal goes from the lower left at Z21 to the upper right at Z12. The determinant of the matrix is the product in the first diagonal minus the product in the second:
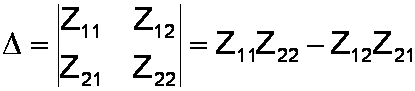
Usually we are only interested in one of the unknown currents, so only one additional determinant is needed. To compute i1 we substitute the column of voltages for the first column of the matrix:
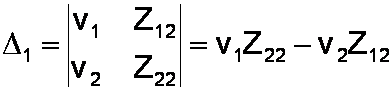
To get i2 we substitute the voltages into the second column:
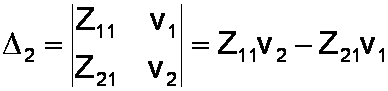
The unknown currents are then
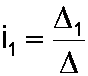
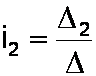

|
Guitar Amplifier Electronics: Circuit Simulation - know your design works by measuring performance at every point in the amplifier. |
Problem
Solve the Sovtek MIG 50 tone stack problem again, but this time using Cramer's Rule.

Solution
We used Kirchhoff's Voltage Law to get the following formulas for the first and second loops:

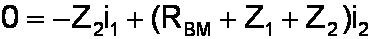
The impedance matrix is thus

The determinant is
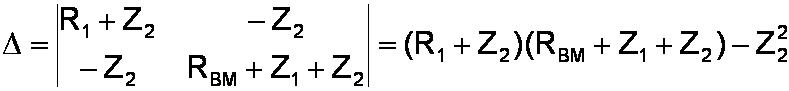
which simplifies to
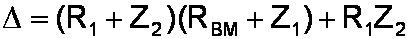
To get i2, we substitute the column of voltages into the second column of the matrix and compute the determinant.
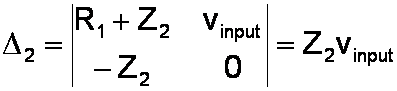
The unknown current is thus
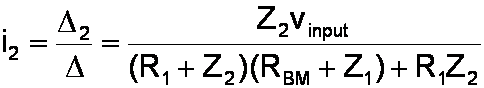
By Ohm's Law the output voltage is RBMi2.
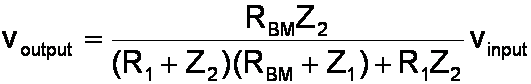
Cramer's Rule takes fewer steps than the substitution method. More importantly, it is far more reliable in practice, because its inherent elegance makes you less likely to make a mistake.
Are we satisfied with a sloppy wiring job that is merely good enough to get the amp to work, or do we want quality workmanship that will guarantee future performance? The same can be said of simple substitution versus Cramer's Rule.

|
From system design concepts to individual stage operation, an all-new examination of Bassman electronics. |


